[LeetCode] 542. 01 Matrix 零一矩阵

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

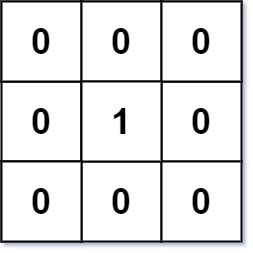
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

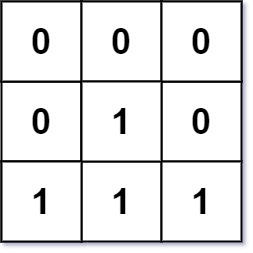
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
There is at least one 0 in mat.

这道题给了一个只有0和1的矩阵，让求每一个1到离其最近的0的距离，其实也就是求一个距离场，而求距离场 BFS 将是不二之选。刚看到此题时，博主以为这跟之前那道 Shortest Distance from All Buildings 是一样的，从每一个0开始遍历，不停的更新每一个1的距离，但是这样写下来超时 TLE 了。后来博主又改变思路，从每一个1开始 BFS，找到最近的0，结果还是 TLE，气死人。后来逛论坛发现思路是对的，就是写法上可以进一步优化，可以首先遍历一次矩阵，将值为0的点都存入 queue，将值为1的点改为 INT_MAX。之前像什么遍历迷宫啊，起点只有一个，而这道题所有为0的点都是起点，这想法，叼！然后开始 BFS 遍历，从 queue 中取出一个数字，遍历其周围四个点，如果越界或者周围点的值小于等于当前值加1，则直接跳过。因为周围点的距离更小的话，就没有更新的必要，否则将周围点的值更新为当前值加1，然后把周围点的坐标加入 queue，参见代码如下：

解法一：

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}};
        queue<pair<int, int>> q;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) q.push({i, j});
                else matrix[i][j] = INT_MAX;
            }
        }
        while (!q.empty()) {
            auto t = q.front(); q.pop();
            for (auto dir : dirs) {
                int x = t.first + dir[0], y = t.second + dir[1];
                if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] <= matrix[t.first][t.second] + 1) continue;
                matrix[x][y] = matrix[t.first][t.second] + 1;
                q.push({x, y});
            }
        }
        return matrix;
    }
};

下面这种解法是参考的 qswawrq 大神的帖子，他想出了一种二次扫描的解法，从而不用使用 BFS 了。这种解法也相当的巧妙，首先建立一个和 matrix 大小相等的矩阵 res，初始化为很大的值，这里用 INT_MAX-1，为甚么要减1呢，后面再说。然后遍历 matrix 矩阵，当遇到为0的位置，将结果 res 矩阵的对应位置也设为0，这 make sense 吧，就不多说了。然后就是这个解法的精髓了，如果不是0的地方，在第一次扫描的时候，比较其左边和上边的位置，取其中较小的值，再加上1，来更新结果 res 中的对应位置。这里就明白了为啥要初始化为 INT_MAX-1 了吧，因为这里要加1，如果初始化为 INT_MAX 就会整型溢出，不过放心，由于是取较小值，res[i][j] 永远不会取到 INT_MAX，所以不会有再加1溢出的风险。第一次遍历比较了左和上的方向，那么第二次遍历就要比较右和下的方向，注意两种情况下不需要比较，一种是当值为0时，还有一种是当值为1时，这两种情况下值都不可能再变小了，所以没有更新的必要，参见代码如下：

解法二：

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> res(m, vector<int>(n, INT_MAX - 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 0) res[i][j] = 0;
                else {
                    if (i > 0) res[i][j] = min(res[i][j], res[i - 1][j] + 1);
                    if (j > 0) res[i][j] = min(res[i][j], res[i][j - 1] + 1);
                }
            }
        }
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                if (res[i][j] != 0 && res[i][j] != 1) {
                    if (i < m - 1) res[i][j] = min(res[i][j], res[i + 1][j] + 1);
                    if (j < n - 1) res[i][j] = min(res[i][j], res[i][j + 1] + 1);
                }
            }
        }
        return res;
    }
};

在史蒂芬大神的帖子中，他提出了一种变型的方法，没有再区分左上右下，而是每次都跟左边相比，但是需要每次把矩阵旋转90度。他用 python 写的解法异常的简洁，貌似 python 中可以一行代码进行矩阵旋转，但是貌似 C++ 没有这么叼，矩阵旋转写起来还是需要两个 for 循环，写出来估计也不短，这里就不写了，有兴趣的童鞋可以自己试试写一下，可以贴到留言板上哈～

Github 同步地址：

https://github.com/grandyang/leetcode/issues/542

类似题目：

Shortest Path to Get Food

参考资料：

https://leetcode.com/problems/01-matrix/

https://leetcode.com/problems/01-matrix/discuss/101021/java-solution-bfs

https://leetcode.com/problems/01-matrix/discuss/101039/java-33ms-solution-with-two-sweeps-in-on

https://leetcode.com/problems/01-matrix/discuss/101023/18-line-c-dp-solution-on-easy-to-understand

https://leetcode.com/problems/01-matrix/discuss/101102/short-solution-each-path-needs-at-most-one-turn

LeetCode All in One 题目讲解汇总(持续更新中...)